Answer:
18 years
Explanation:
The formula for computing accrued amount A for a principal of P at an interest rate of r(in decimal) compounded n times in a year for t years is given by
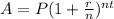
Note that r is percentage converted to decimal. So 3% = 3/100 = 0.03
We can rearrange the above equation to:
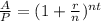
Taking logs on both sides
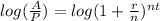
This gives
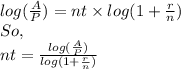
In this particular problem, n = 4, , A= 9600, P = 5600, r =0.03, so r/n = 0.03/4 = 0.0075
1 + r/n = 1+0.0075 = 1.0075
4t = log(9600/5600)/log(1.0075) = log(1.714) / log(1.0075) = 0.234 /0.00325 = 72
t = 72/4 = 18 years