Question

ALGEBRA 2

There were 350 tickets sold for the spring concert at the local high school. Adult tickets cost $4.00 each, student tickets cost $2.50 each, and senior tickets cost $2.00 each. There were 40 fewer senior tickets sold than student tickets. If a total of$1,095 was collected from tickets, write the linear systems that could be used to find the number of each type of ticket sold

Answer 1

`\left\{ \begin{array}{ll} a+s+r=350 \\ 4a+2.5s+2r=1095\\r=s-40 \end{array} \right.`

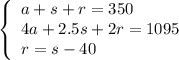
Explanation:

Let's define our variables. Let a represent the number of adult tickets sold, s represent the number of senior tickets sold, and r represent the number of senior tickets sold.

We know that a total of 350 tickets were sold. So, the number of adult, student, and senior tickets sold must total 350. Therefore, we can write the following equation:

`a+s+r=350`

We know that each adult ticket costs $4, each student ticket costs $2.50, and each senior ticket costs $2. We are given that a total of $1095 was collected. Therefore, the number of tickets multiplied by their respective price must equal $1095. So, we can write the following equation:

`4a+2.5s+2r=1095`

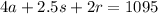
Finally, we know that 40 fewer senior tickets were sold than student tickets. So, however many students tickets were sold, we can subtract 40 to get the number of senior tickets sold. Therefore:

`r=s-40`

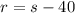
So, our system of equations is:

`\left\{ \begin{array}{ll} a+s+r=350 \\ 4a+2.5s+2r=1095\\r=s-40 \end{array} \right.`

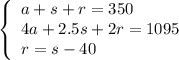
And we're done!