Answer:
98,000 bacteria.
Explanation:
We are given the formula:
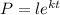
Where l is the initial population, k is the rate of growth, and t is the time ( in hours).
We know that it has an initial population of 500. So, l is 500.
We also know that the population grows to 7000 after 2 hours.
And we want to find the population after 4 hours.
First, since we know that the population grows to 7000 after 2 hours, let's substitute 2 for t and 7000 for P. Let's also substitute 500 for l. This yields:
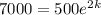
Divide both sides by 500:
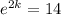
We can solve for the rate k here, but this is not necessary. In fact, when can find our solution with just this.
Let's go back to our original equation. We want to find the population after 4 hours. So, substitute 4 for t:
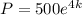
We want to find the total population, P. Notice that we can rewrite our exponent as:
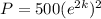
This is the exact same thing we acquired earlier. So, we know that the expression within the parentheses is 14. Substitute:
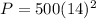
Square and multiply:
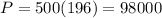
So, after 4 hours, there will be 98,000 bacteria.
And we're done!