Question

Which of the following is the equation of the line that is parallel to

y= 3/5x+ 8 and goes through point (-10,4)?
Select one:
a. y = 5/3x + 20 2/3
b. y=-5/3x – 12 2/3
c.y= 3/5x + 10
d. y = -3/5x-2

Answer 1

Explanation:

Hey there!

The equation of a st.line passing through point (-10,4) is ;

(y-y1)= m1(x-x1) [one point formula]

Put all values.

(y - 4) = m1( x + 10)..........(i)

Another equation is; y = 3/5 + 8.............(ii)

From equation (ii)

Slope (m2) = 3/5 [ By comparing equation with y = mx+c].

As per the condition of parallel lines,

Slope of equation (i) = slope of equation (ii)

(i.e m1 = m2 )

Therefore, the value of m1 is 3/5.

Putting value of slope in equation (i).

`(y - 4) = (3)/(5) (x + 10)`

`(y - 4) = (3)/(5) x + (3)/(5) * 10`

`(y - 4) = (3)/(5) x + 6`

`y = (3)/(5) x + 10`

Therefore the required equation is y = 3/5x + 10.

Hope it helps...

Answer 2

C

Explanation:

We want to write the equation of a line that is parallel to:

`y=(3)/(5)x+8`

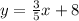
And also passes through (-10, 4).

Remember that parallel lines have the same slope.

The slope of our old line is 3/5.

Therefore, the slope of our new line is also 3/5.

We know that it passes through (-10, 4). So, we can use the point-slope form:

`y-y_1=m(x-x_1)`

Where m is the slope and (x₁, y₁) is a point.

So, let's substitute 3/5 for m and let (-10, 4) be our (x₁, y₁). This yields:

`y-(4)=(3)/(5)(x-(-10))`

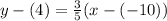
Simplify:

`y-(4)=(3)/(5)(x+10)`

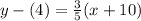
Distribute on the right:

`y-4=(3)/(5)x+6`

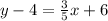
Add 4 to both sides:

`y=(3)/(5)x+10`

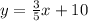
So, our answer is C.

And we're done!