Answer:

Explanation:
First determine whether it is a sine function or a cosine function. Since
sin(x) = 0 at x = 0 and we see indeed that the value of the function is 0 at x = 0 it must be a sine function
The general equation of a sine function is
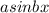
where a is the amplitude. The amplitude is one-half the difference between the lowest and highest values in the graph.From the graph we can see that the highest value is 3/4 and lowest is -3/4 so the amplitude = 1/2 (3/4 + 3/4) = 3/4
If the amplitude were positive, the function would be increasing at (0,0) and going up to its amplitude value. However we can see that the function is decreasing at (0,0 ) and goes down to -3/4. Therefore the amplitude a has a negative sign so a = -3/4
To compute b, note that the period of the function ie where it finishes a full cycle is 3π since the function at that x value repeats itself. The relationship between b and the period is 2π/b = 3π in this particular case
This gives b = 2/3
So a = -3/4, b = 2/3 and the equation is
