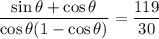Question

Tan theta equals 8 / 15 find sine theta + cos theta / cos theta (1 - cos theta)​

Answer 1

I guess you have to find

`(\sin\theta+\cos\theta)/(\cos\theta(1-\cos\theta))`

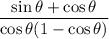
given that
`\tan\theta=\frac8{15}`.

We can immediately solve for
`\sec\theta`:

`\sec^2\theta=1+\tan^2\theta\implies\sec\theta=\pm(17)/(15)`

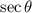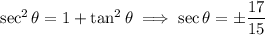
(without knowing anything else about
`\theta`, we cannot determine the sign)

Then we get
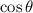`\cos\theta` for free:

`\cos\theta=\frac1{\sec\theta}=\pm(15)/(17)`

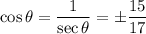
and we can now solve for
`\sin\theta`:

`\sin^2\theta+\cos^2\theta=1\implies \sin\theta=\pm\frac8{17}`

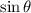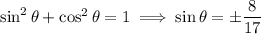
Notice that we have 2*2 = 4 possible choices of sign for either sin or cos.

• If both are positive, then

`(\sin\theta+\cos\theta)/(\cos\theta(1-\cos\theta))=(391)/(90)`

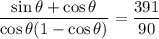
• If both are negative, then

`(\sin\theta+\cos\theta)/(\cos\theta(1-\cos\theta))=(391)/(480)`

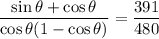
• If sin is positive and cos is negative, then

`(\sin\theta+\cos\theta)/(\cos\theta(1-\cos\theta))=(119)/(480)`

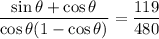
• If cos is positive and sin is negative, then

`(\sin\theta+\cos\theta)/(\cos\theta(1-\cos\theta))=(119)/(30)`