Question

If 12 cats can catch 6 rats in 2 hours, how many hours would it take 50 cats to catch 75 rats?

Answer 1

50 cats would take 6 hours to catch 75 rats.

Explanation:

After reading the statement we noticed the existence of two relationships:

1) The amount of cats is directly proportional to the quantity of caught rats.

2) The amount of cats is inversely proportional to time taken to catch rats.

That is to say:

`n \propto (x)/(y)`

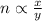
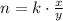`n = k\cdot (x)/(y)` (Eq. 1)

Where:

`n` - Amount of cats, dimensionless.

`x` - Amount of caught rats, dimensionless.

`y` - Time, measured in hours.

`k` - Proportionality ratio, measured in hours.

Then, we obtain the following relationship by eliminating the proportionality ratio in (Eq. 1):

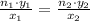`(n_(1)\cdot y_(1))/(x_(1)) = (n_(2)\cdot y_(2))/(x_(2))` (Eq. 2)

Where:

`n_(1)`,
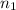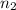`n_(2)` - Initial and final amounts of cats, dimensionless.

`x_(1)`,
`x_(2)` - Initial and final amounts of caught rats, dimensionless.

`y_(1)`,
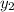`y_(2)` - Initial and final times, measured in hours.

Now we clear final time in (Eq. 2):

`y_(2) = y_(1)\cdot \left((n_(1))/(n_(2)) \right)\cdot \left((x_(2))/(x_(1)) \right)`

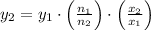
By knowing that
`y_(1) = 2\,h`,
`n_(1) = 12`,
`x_(1) = 6`,
`n_(2) = 50`,
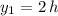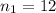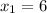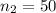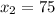`x_(2) = 75`, then we get that time taken by 50 cats to catch 75 rats is:

`y_(2) = (2\,h)\cdot \left((12)/(50) \right)\cdot \left((75)/(6)\right)`

`y_(2) = 6\,h`

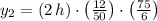
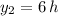
50 cats would take 6 hours to catch 75 rats.