Question

The length of a rectangular garden is 5 feet less than 4 times its width. Its area is 359 square feet. Find the length and width of the garden. Round answers to the nearest tenth of a foot. Show all work.

Answer 1

Given parameters:

Area of the rectangular garden = 359ft²

Unknown:

length and width of the garden = ?

To find the length and breadth of the garden, we need to define and know that the area of a rectangle is.

Area of a rectangle = Length x Breadth

From the problem statement;

Let w = width of the rectangular garden

L = length of the garden;

Now,

length of a rectangular garden is 5 feet less than 4 times its width

L = 4w - 5

Now let us substitute this into the equation;

Area = L x w

359 = (4w - 5)w

4w² - 5w - 359

Using:

w = -b ± √b² - 4ac / 2a

where b = -5 , a = 4 and c = -359

w = -(-5) ± √-5² - 4(4)(-359) / 2(4)

w = 5 ± √25 + 5744 / 8

w = 5 ± 75.9 / 8

w =
`(5 + 75.9)/(8) or (5 - 75.9)/(8)`

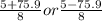
w = 10.1ft

The other solution is not possible it will be a negative value. Width value cannot be negative.

So L = 4w - 5 = 4(10.1) - 5 = 35.5ft

The length and breadth of the rectangular are 35.5ft and 10.1ft respectively.