Answer:
The 7th person weighted 117
Explanation:
Average Value
The mean or average of a number n of measurements is defined as the sum of all values divided by n.
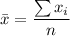
The question gives us some input data. The average weight of n=6 people is
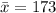 . With this information, we can set this relationship:
. With this information, we can set this relationship:
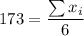
From the above equation, we know the sum of the first 6 persons:
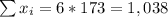
When a 7th person gets on, the new average gets down to 165 and n=7. The equation for the new average is:

Note we have a new summand to the numerator. It's the weight of the 7th person. Let's solve for X:

Multiply by 7:

Operate and swap sides:
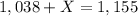

The 7th person weighted 117