Problem 4
- a = 10800 = initial population
- b = 1 + r = 1 + (-0.025) = 0.975 is the decay factor
The template of
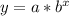 becomes
becomes
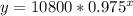 to represent the exponential function.
to represent the exponential function.
- x = number of years since 2002
- y = population
We want to know when the population reaches half of 10800, so we want to know when the population is 10800/2 = 5400
Plug in y = 5400 and solve for x.
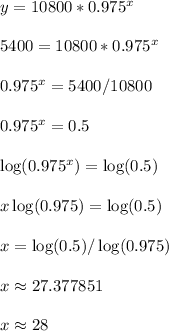
I rounded up to the nearest whole number because x = 27 leads to y = 5452, which is not 5400 or smaller.
Luckily, x = 28 leads to y = 5315 which gets over the hurdle of being 5400 or smaller.
Add 28 years onto the starting year 2002 and we get to 2002+28 = 2030
The population reaches half of its original amount in the year 2030.
Answers:
- The exponential function is
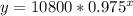
- It takes 28 years to get to half the population. This occurs in the year 2030
============================================================
Problem 5
- a = 28750 = starting value for the car
- b = 1 + r = 1 + (-0.12) = 0.88 = decay factor
If the car loses 12% of its value each year, then it keeps the remaining 88%
Plug those values into
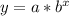 .
.
We find the equation is
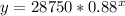 where,
where,
- x = number of years since 2012
- y = car's value
Replace y with 10,000 and solve for x.

Like in the previous problem, we round up so we clear the hurdle.
Adding 9 years onto 2012 gets us to 2012+9 = 2021
Answers:
- The function is
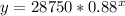
- It takes about 9 years, and it occurs in the year 2021