Problem 1
a = 2500 = starting amount
b = 1 + r = 1 + 0.035 = 1.035 = growth factor
The equation is
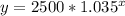 as it is in the form
as it is in the form
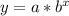
Plug in y = 5000 and solve for x.
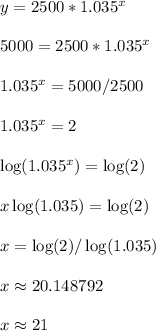
I rounded up to get over the hurdle. This is because plugging x = 20 will lead to y being smaller than $5000, so we must use x = 21.
Answers:
- The function is
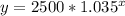
- It takes about 21 years to reach $5000
=========================================================
Problem 2
a = 4.22 = starting amount
b = 1 + r = 1 + 0.031 = 1.031 = growth factor
The equation goes from
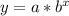 to
to
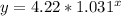
Plug in y = 9.33 and solve for x.

Answers:
- The function is
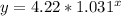
- It takes about 26 years for the ticket to reach the price of $9.33
=========================================================
Problem 3
a = 400 = initial value
b = 1 + r = 1 + 0.25 = 1.25 = growth factor
The template
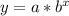 updates to
updates to
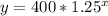
Plug in y = 3000 and isolate x.
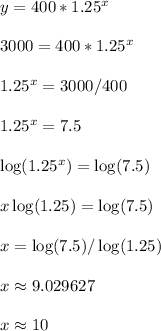
Like with the first problem, I rounded up to the nearest whole number. If you tried out x = 9, then y = 2980 approximately which is short of the goal of 3000. Trying x = 10 leads to y = 3725 approximately, which is now over the goal we're after.
Answers:
- The function is
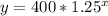
- It takes about 10 days for 3000 people to get infected.