Question

What is the value of x?

Input Output
1 5
2 7
3 9
Х 17

Answer 1

to get the equation of any straight line, we simply need two points off of it, so let's use the points in the picture below.

`(\stackrel{x_1}{1}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{3}~,~\stackrel{y_2}{9}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{9}-\stackrel{y1}{5}}}{\underset{run} {\underset{x_2}{3}-\underset{x_1}{1}}}\implies \cfrac{4}{2}\implies 2 \\\\\\ \begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{5}=\stackrel{m}{2}(x-\stackrel{x_1}{1})`

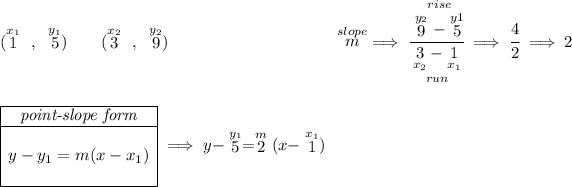
now, if we use the last point from the table, namely (x , 17), we can see that x = x and y = 17, so let's plug those in the equation

`(17)-5=2(x-1)\implies 12=2x-2\implies 14=2x\implies \cfrac{14}{2}=x\implies 7=x \\\\[-0.35em] ~\dotfill\\\\ ~\hfill (7~~,~~17)~\hfill`