Question

In​ 2012, the population of a city was 6.63 million. The exponential growth rate was 3.01​% per year.

​a) Find the exponential growth function.
​b) Estimate the population of the city in 2018.
​c) When will the population of the city be 11 ​million?
​d) Find the doubling time.

Answer 1

So first we need to determine what the exponential growth function would look like. Exponential growth functions look like
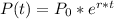`P(t) = P_0*e^(r*t)` and in our case
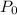`P_0` would be the initial population which is 6.63 million. R is the next variable that we need to fill out which is the rate of change which in our case is 3.01% or 0.0301.

This is how our function should look now
`P(t)=6.63*e^(0.0301*t)`

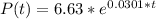
Moving onto part b, we need to estimate the population of the city in 2018 which 6 years from 2012 and we plug that into t and solve.

`P(t) = 6.63 * e^(0.0301*6)`

`P(t) = 6.63*e^(0.1806)`

`P(t) = 6.63 *1.1979`

`P(t) = 7.9423\ million`

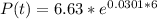
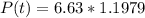
Moving onto part c, we need to find when the population of the city will be 11 million which will be done by setting P(t) to 11 million and solving for t.

`11 = 6.63*e^(0.0301*t)`

`(11)/(6.63) = (6.63*e^(0.0301*t))/(6.63)`

`1.659=e^(0.0301*t)`

`ln(1.659)=ln(e^(0.0301*t))`

`(0.506)/(0.0301)=(0.0301*t)/(0.0301)`

`16.818\ years = t`

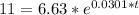
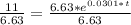
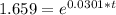
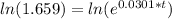
Moving onto part d, we need to find the doubling time. This will be similar to the previous part but we will be finding the time it takes to double our population. So instead of putting 11 million for P(t) we put 6.63 * 2 in there which is 13.26.

`13.26 = 6.63*e^(0.0301*t)`

`(13.26)/(6.63) = (6.63*e^(0.0301*t))/(6.63)`

`2=e^(0.0301*t)`

`ln(2)=ln(e^(0.0301*t))`

`(0.693)/(0.0301)=(0.0301*t)/(0.0301)`

`23.028\ years = t`

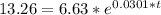
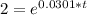
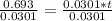
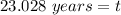
Hope this helps! Let me know if you have any questions