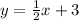Answer:
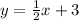
Explanation:
Using the given points, first find the slope:
m = (₂ - y₁) / (x₂ - x₁)
= (5 - 9) / (-1 - (-3))
= -4 / 2
= -2
Find y-intercept by using anyone of the give points and slope from above:
y = mx + b
5 = -2(-1) + b
5 = 2 + b
b = 3
With the m and b, you can make equation of line:
y = mx + b
y = -2x + 3
To find the perpendicular slope, make it opposite and inverse it.
m = -2 becomes 1/2
Regular equation of line:
y = -2x + 3
Perpendicular equation of line: