Answer:
Explanation:
You can rewrite the given log expressions to express them in terms of ln(a), ln(b), and ln(c). Then substituting the given values will produce the value of the expression.
Or, you can define the variables 'a', 'b', and 'c' and let your calculator compute these directly.
__
1.
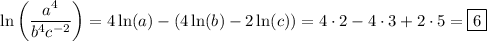
2.
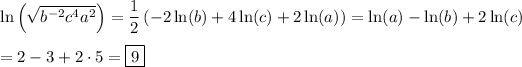
3.
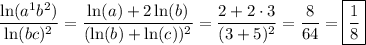
4.
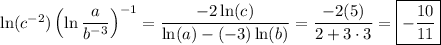
_____
The applicable rules of logarithms are ...
- ln(ab) = ln(a) +ln(b)
- ln(a/b) = ln(a) -ln(b)
- ln(a^b) = b·ln(a)
- ln(a) = b ⇔ a = e^b
Of course, a square root is the same as a 1/2 power.