Answer:
A. Division property of inequality.
Explanation:
Let be
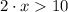 , we proceed to show the appropriate procedure to step 4:
, we proceed to show the appropriate procedure to step 4:
1)
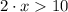 Given
Given
2)
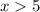 Compatibility with multiplication/Existence of multiplicative inverse/Associative property/Modulative property/Result. (Division property of inequality)
Compatibility with multiplication/Existence of multiplicative inverse/Associative property/Modulative property/Result. (Division property of inequality)
In consequence, the division property of inequality which states that:
 . If
. If
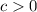 , then:
, then:
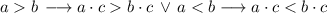
But if
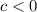 , then:
, then:
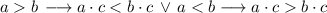
Hence, correct answer is A.