Answer:
D. Rotation 270 degrees clockwise.
Explanation:
The transformation used in the coordinates below was a rotation 270 degrees clockwise, whose definition is:
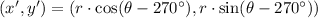
Please note that clockwise rotation is represented by the minus sign.
Where
 is the norm of original point, defined as:
is the norm of original point, defined as:
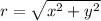 ,
,
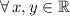
And
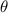 is the direction of the point centered at origin and with respect to +x semiaxis, measured in sexagesimal degrees:
is the direction of the point centered at origin and with respect to +x semiaxis, measured in sexagesimal degrees:
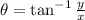
Now we proceed to prove the statement:
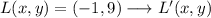
Norm
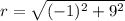
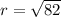
Direction
The point is located on 2nd quadrant, which means that
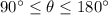 . Then:
. Then:
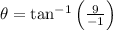
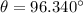
Rotation
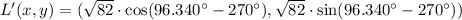
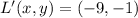
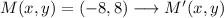
Norm
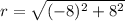
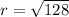
Direction
The point is located on 2nd quadrant, which means that
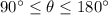 . Then:
. Then:
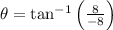
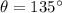
Rotation
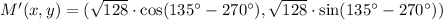
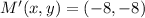
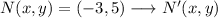
Norm
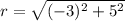
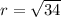
Direction
The point is located on 2nd quadrant, which means that
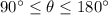 . Then:
. Then:
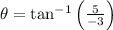
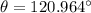
Rotation
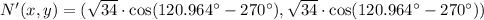
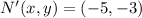
Hence, the correct answer is D.