Question

How many grams of water at 5.00 °C would we need to mix with 140.0 g of water at 85.0 °C to obtain a final temperature of 43.0 °C ?

Answer 1

We need 154.737 grams of water at 5 ºC to obtain a final temperature of 43 ºC.

Step-by-step explanation:

From Thermodynamics we know that mixing processes involve the interaction of substance at different temperatures so that thermal equilibrium is reached by cooling down the substance with highest temperature and heating up the subtance with lowest temperature.

Let suppose that mixing occurs at steady state, that is, that system does not have energy interactions with surroundings. According to the First Law of Thermodynamics, we get that energy interactions are represented by:

`H_(L) + H_(H) -H_(R) = 0`

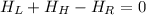
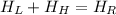`H_(L) + H_(H) = H_(R)` (Eq. 1)

Where:

`H_(L)` - Enthalpy of cold water, measured in joules.

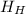`H_(H)` - Enthalpy of hot water, measured in joules.

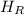`H_(R)` - Enthalpy of mixed water, measured in joules.

Since there are no phase changes, we can expand formula by using the definition of sensible heat. That is:

`m_(L)\cdot c_(w)\cdot T_(L)+m_(H)\cdot c_(w)\cdot T_(H) = m_(R)\cdot c_(w)\cdot T_(R)`

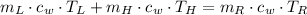
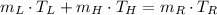`m_(L)\cdot T_(L)+m_(H)\cdot T_(H) = m_(R)\cdot T_(R)` (Eq. 2)

Where:

`m_(L)`,
`m_(H)`,
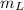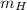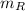`m_(R)` - Masses of cold, hot and mixed water, measured in grams.

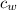`c_(w)` - Specific heat of water, measured in joules per gram-Celsius.

`T_(L)`,
`T_(H)`,
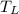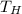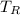`T_(R)` - Temperatures of cold, hot and mixed water, measured in Celsius.

But we know from Principle of Mass Conservation that:

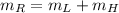`m_(R) = m_(L)+m_(H)` (Eq. 3)

Then, we simplify (Eq. 2) and clear the mass of cold water:

`m_(L)\cdot T_(L)+m_(H)\cdot T_(H) = (m_(L)+m_(H))\cdot T_(R)`

`m_(H)\cdot (T_(H)-T_(R)) = m_(L)\cdot (T_(R)-T_(L))`

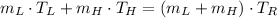
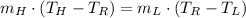
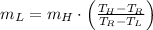`m_(L) = m_(H)\cdot \left((T_(H)-T_(R))/(T_(R)-T_(L)) \right)` (Eq. 4)

If we know that
`m_(H) = 140\,g`,
`T_(L) = 5\,^(\circ)C`,
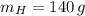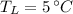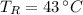`T_(R) = 43\,^(\circ)C` and
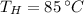`T_(H) = 85\,^(\circ)C`, the mass of cold water needed to obtain a final temperature is:

`m_(L) = (140\,g)\cdot \left((85\,^(\circ)C-43\,^(\circ)C)/(43\,^(\circ)C-5\,^(\circ)C) \right)`

`m_(L) = 154.737\,g`

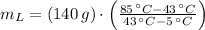
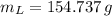
We need 154.737 grams of water at 5 ºC to obtain a final temperature of 43 ºC.