Question

In ten-pin bowling, the highest possible score in a single game is 300. At one point in the bowling season, Fred F Stone had an average score of 177. In his next game he obtained a score of 199, which caused his average to increase to. 178. After one more game Fred would like his average to be 183. Is it possible for Fred

Answer 1

Let, number of games played is n and sum of their points are x.

So,
`177=(x)/(n)`

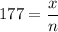
Now, In his next game he obtained a score of 199, which caused his average to increase to 178.

`178=(x+199)/(n+1)`

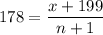
Now equations are :

x = 177n ...1)

x + 199 = 178( n + 1 )

x = 178n - 21 ...2)

Solving eq 1 and 2 , we get :

x = 3717 and n = 21 .

Now, new average is 183.

Let, point scored in last game is y.

So,

`183 =(x+y)/(n+1+1)\\\\183 = (3717+y)/(23)\\\\y = 183* 23 - 3717\\\\y=492`

He required 492 points which is greater than the maximum i.e 300.

Therefore, it is not possible for Fred.

Hence, this is the required solution.