Question

Astronomers treat the number of stars X in a given volume of space as Poisson random variable. The density of stars in the Milky Way Galaxy in the vicinity of our solar system is one star per 16 cubic light-years, on average. NOTE: Light-years is a distance measure. 7. What is the probability of exactly two stars in 16 cubic light-years? 8. What is the probability of three or more stars in 16 cubic light-years? 9. How many stars would be expected in 4 cubic light years? 10. How many stars would be expected in t cubic light years? 11. How many cubic light-years of space must be studied so that the probability of one or more stars exceeds 0.95? HINT: let `t' represent the unknown region of space, then nd the `t' that gives you the relevant probability.

Answer 1

Explained below.

Explanation:

The random variable X is defined as the number of stars in a given volume of space.

`X\sim \text{Poisson}\ (\lambda=1)`

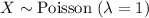
The probability mass function of X is:

`p_(X)(x)=(e^(-\lambda)\lambda^(x))/(x!)`

(7)

Compute the probability of exactly two stars in 16 cubic light-years as follows:

`P(X=2)=(e^(-1)* 1^(2))/(2!)=(e^(-1))/(2)=(0.36788)/(2)=0.18394\approx 0.184`

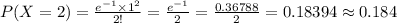
(8)

Compute the probability of three or more stars in 16 cubic light-years as follows:

`P(X\geq 3)=1-P(X<3)\\\\=1-P(X=0)-P(X=1)-P(X=2)\\\\=1-\sum\limits^(2)_(x=0)[(e^(-1)* 1^(x))/(x!)]\\\\=1-0.36788-0.36788-0.18394\\\\=0.0803`

(9)

In 16 cubic light years there is only 1 star.

Then in 1 cubic light years there will be, (1/16) stars.

Then in 4 cubic light years there will be, 4 × (1/16) = (1/4) stars.

(10)

In 16 cubic light years there is only 1 star.

Then in 1 cubic light years there will be, (1/16) stars.

Then in t cubic light years there will be, [t × (1/16)] stars.