Question

Jubal wrote the four equations below. He examined them, without solving them, to determine which equation has no solution. 7 x + 1 = 7 x+ 1. 3 x + 2 = 3 x minus 2. 4 x + 1 = 3 x + 8. Negative 2 x minus 1 = negative 2 x minus 1. Which of Jubal's equations has no solution? 7 x + 1 = 7 x+ 1 3 x + 2 = 3 x minus 2 4 x + 1 = 3 x + 8 negative 2 x minus 1 = negative 2 x minus 1

Answer 1

D

Explanation:

Answer 2

Given:

Four equations are

`7 x + 1 = 7 x+ 1`

`3 x + 2 = 3 x-2`

`4 x + 1 = 3 x + 8`

`-2x-1 = -2 x-1`

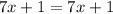
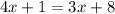
To find:

Without solving which equation has no solution.

Solution:

We know that, in an equation

1. No solution : When variable terms are same but constants are different.

2. Unique solution : When variable terms are different.

3. infinitely many solution : When variable terms and constants are same.

In first and fourth equations, terms on left sides are equal to the terms on the right side. So, LHS = RHS for any value of x.

Therefore, these two equations (first and fourth) have infinitely many solutions.

In second equation, variable terms are same on both sides, but the constants are difference. So, LHS ≠ RHS for any value of x.

Therefore, the second has no solutions.

In third equation, coefficient of x are difference on both sides.

So, this equation has unique solution.

Therefore, Jubal's equations
`3 x + 2 = 3 x-2` has no solution. Hence, the correct option is B.