Answer:
The correct answer is:
x = 15
y = 63
Defining Key Terms
To begin, an understanding of the types of angles must be established.
- Alternate Interior Angles: Alternate interior angles are angles that oppose one another and are interior (not on the outside of the transversal/figure). An example is supplied in the image. In this instance, the angle measurements (9x - 7)° and (2y + 2)° are alternate interior angles.
- Supplementary Angles: Supplementary angles are situated on the same straight line, on the same side of the straight line, and add up to 180° measurements. In this instance, the angle measurements (4x - 8)° and (9x - 7)° are supplementary angles.
Solve - Supplementary Angles (x-term)
An equation can be devised since both angle measurements will equal 180°. It can be said that:
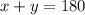
Assigning a variable to an angle measurement (the assignment does not matter in this scenario):
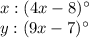
Then, substitute the new values into the devised equation:

Then, drop the parentheses and combine like terms:

Then, add 15 to both sides of the equation to isolate the term hosting the variable:
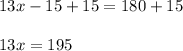
Finally, divide by 13 on both sides to isolate the variable:
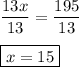
Therefore, x = 15.
Then, substitute the x-value into the angle measurement (9x - 7) to solve for the angle measurement in degrees:

Solve - Alternate Interior Angles (y-term)
Then, using the new measurement for the angle alternate to (2y + 2)°, since alternate interior angles are congruent (equal), an equation can be devised that sets the unknown angle equal to the known angle:
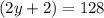
Then, subtract 2 from both sides to isolate the term hosting the variable:
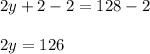
Finally, divide both sides by 2 to isolate the variable:
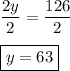
Therefore, y = 63.
Final Answer
Therefore, x = 15 and y = 63.