Question

What is the value of "c" in the following quadratic? (Make sure the equation is in

standard form: ax^2 + bx +c= 0)
X^2 +28 = -11x

Answer 1

`\rule{50}{1}\large\blue\textsf{\textbf{\underline{Given question:-}}}\rule{50}{1}`

What is the value of c in the quadratic
`\large\text{$x^2+28=-11x$}`?

`\rule{50}{1}\large\textsf{\textbf{\underline{Answer and how to solve:-}}}\rule{50}{1}`

Before starting to solve, you should notice something - the

quadratic is not in its standard form!

We can easily fix it by adding
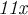`\large\textit{11x}` on both sides:-

`\large\text{$x^2+28-11x=0$}`

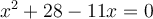
We can switch the order of 28 and -11x:-

`\large\text{$x^2-11x+28=0$}`

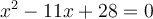
Now, the quadratic is in its standard form, so we can get down to

finding the value of "c".

Remember, the standard form of a quadratic looks like so:-

• 
  `\large\text{$ax^2+bx+c=0$}`

Now we can just write our quadratic here:-

• 
  `\large\text{$x^2-11x+28=0$}`

Now, can you see what the value of "c" is?

An easy way to remember "c" in quadratics is:-

The "c" in quadratics is the constant.

Henceforth, we conclude that the value of "c" in the given quadratic is:-

`\Large\textbf{28}\Large\checkmark`

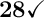
Good luck with your studies.

`\rule{50}{1}\smile\smile\smile\smile\smile\smile\rule{50}{1}`