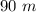Question

Picture a long, straight corridor running east-west, with a water fountain located somewhere along it. Starting from the west end of the corridor, a woman walks a short distance east along the corridor and stops before reaching the water fountain. The distance from her to the fountain is twice the distance she has walked. She then continues walking east, passes the water fountain, and stops 60 m from her first stop. Now the distance from her to the fountain is twice the distance from her to the east end of the corridor. How long is the corridor

Answer 1

The corridor's distance is "90 m".

Step-by-step explanation:

• She heads in the east directions but creates the first pause, meaning she crosses the distance 'x' in step 1.
• Now, provided that perhaps the distance by her to another fountain or waterfall just after the first stop is twice as far away she traveled.
• Because she moved the distance of 'x,' then, therefore, her distance towards the fountain of '2x.' She casually strolls and once again pauses 60 m beyond her stop.
• The gap about her to the waterfall during that time approximately twice the distance and her to the eastern end of the hallway.
• Assume her gap from either the east end of the platform seems to be 'y' at either the second stop, after which '2y' may become the distance between the 2nd pause and the waterfall.

Now,

⇒
`2x + 2y = 60`

⇒
`x + y = 30`

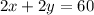
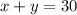
The total distance of the corridor will be:

=
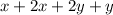
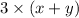
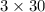
`x + 2x + 2y + y`

=
`3* (x + y)`

=
`3* 30`

=
`90 \ m`