The question is missing parts. The complete question is here.
The human circulatory system is closed, that is, the blood pumped out of the left ventricle of the heart into the arteries is constrained to a series of continuoous, branching vessels as it passes through the capillaries and then into the veins as it returns to the heart. The blood in each of the heart's four chambers comes briefly to rest before it is ejected by cotraction of the heart muscle. If the aorta (diameter
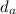 ) branches into two equal-sized arteries with a combined area equal to that of the aorta, what is the diameter of one of the branches?
) branches into two equal-sized arteries with a combined area equal to that of the aorta, what is the diameter of one of the branches?
(a)
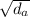
(b)
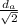
(c)
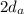
(d)

Answer: (b)
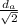
Explanation: The cross-sectional area of a vessel is a circle. So area is:

Radius is half of a diameter, i.e.:
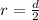
Suppose
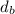 is diameter of the branches, radius of one the branches is:
is diameter of the branches, radius of one the branches is:
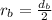
Both branches are equal sized, which means, both have the same radius. So, combined area of both branches is:
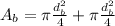
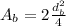
Area of aorta is
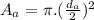
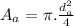
Area of aorta is equal the combined area of the branches, then:

Rearraging:

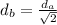
The diameter of one of the branches is
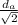 .
.