Question

As mentioned in problem 1.2 from Chapter 1, if you stand on one leg the load exerted on the hip joint is 2.4 times your body weight. Assuming a simple cylindrical model for the implant, calculate the corresponding stress (in MPa) on a hip implant in a individual with a hip implant with a cross-sectional area of If the hip implant is made of Ti6Al4V (124 GPa elastic modulus), what is the strain for the given loading conditions?

Answer 1

The question is incomplete. Here is the complete question.

As mentioned in problem 1.2 from Chapter 1, if you stand on one leg the load exerted on the hip jpint is 2.4 times your body weight. Assuming a simple cylindrical model for the implant, calculate the corresponding stress (in MPa) on a hip implant in a 175lb individual with a hip implant with cross-sectional area of 5.6cm². If the implant is made of Ti6AI4V (124 GPa elastic modulus), what is the atrain for the given loading conditions?

Answer: σ = 3.336 MPa

Strain = 2.69.
`10^(-5)`

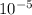
Step-by-step explanation: Stress is the measurement of how hard a weight works to change a material's shape. Its symbol is σ and is calculated as

`\sigma = (F)/(A)`

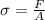
where

F is force

A is cross sectional area

For the hip implant, force is 2.4x of an 175lb individual:

F = 2.4 * 175

F = 420lb

As the question is asking for Pa and 1 Pa = 1 N/m², transform lb in Newtons:

F = 420lb * 4.448N/lb

F = 1868 N

And cm² in m²:

A =
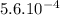`5.6.10^(-4)` m²

Calculating Stress:

`\sigma=(1868)/(5.6.10^(-4))`

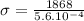
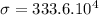`\sigma=333.6.10^(4)` Pa

or

σ = 3.336 MPa

Stress on a hip implant of an individual with weight 175lb is 3.336 MPa.

Strain is the measure of the deformation of a material due to a load. It can be calculated as:

strain =
`(stress)/(modulus)`

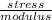
But first, change MPa into GPa:

3.336 MPa =
`3.336.10^(-3)` GPa

strain =
`(0.003336)/(124)`

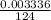
strain =
`2.69.10^(-5)`

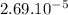
Ti6Al4V is a titanium alloy used in implants. So, the strain the alloy does on a hip implant of a 175lb individual is
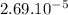`2.69.10^(-5)`.