Answer:
The answer is below
Step-by-step explanation:
A What is the probability that all 4 selected workers will be the day shift?
B What is the probability that all 4 selected workers will be the same shift?
C What is the probability that at least two different shifts will be represented among the selected workers.
A)
The total number of workers = 10 + 8 + 6 = 24
The probability that all 4 selected workers will be the day shift is given as:
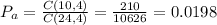
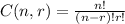
B) The probability that all 4 selected workers will be the same shift (
 ) = probability that all 4 selected workers will be the day shift + probability that all 4 selected workers will be the swing shift + probability that all 4 selected workers will be the graveyard shift.
) = probability that all 4 selected workers will be the day shift + probability that all 4 selected workers will be the swing shift + probability that all 4 selected workers will be the graveyard shift.
Hence:
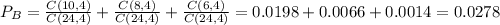
C) The probability that at least two different shifts will be represented among the selected workers (
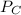 )= 1 - the probability that all 4 selected workers will be the same shift(
)= 1 - the probability that all 4 selected workers will be the same shift(
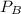 )
)
