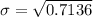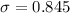Answer:
Yes the table shows a probability distribution
The mean is
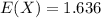
The standard deviation is
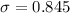
Explanation:
From the question we are told that
The data given is
x 0 1 2 3
P(x) 0.087 0.344 0.415 0.154
Generally we can evaluate
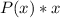 as
as
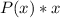 0 (1 * 0.344 ) (2 * 0.415) (3 * 0.154 )
0 (1 * 0.344 ) (2 * 0.415) (3 * 0.154 )
=>
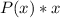 0 0.344 0.830 0.462
0 0.344 0.830 0.462
Generally we can evaluate
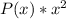 as
as
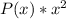 0 [tex ](1^2 * 0.344 )[/tex] [tex ](2^2 * 0.415)[/tex] [tex ](3^2 * 0.154 )[/tex]
0 [tex ](1^2 * 0.344 )[/tex] [tex ](2^2 * 0.415)[/tex] [tex ](3^2 * 0.154 )[/tex]
=>
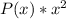 0
0
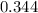 [tex ]1.66 [/tex]
[tex ]1.66 [/tex]
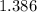
Generally the mean is mathematically represented as
![E(X) = \sum [x* P(x)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/bpicwswmbyxew9yn414zw3jrzv6z5uh3sh.png)

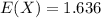
Generally the standard deviation is mathematically represented as
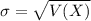
Here
 is the variance which is mathematically represented as
is the variance which is mathematically represented as
![V(X) = [E(X^2) ]- [E(X)]^2](https://img.qammunity.org/2021/formulas/mathematics/high-school/eg2lxiqjufkaaxqqcc9nly72ws162aamik.png)
Here
![E(X^2) = \sum [x^2 * P(x)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/hmbzkxosvuu6zxoyzxis0lcpdlw3crcki3.png)
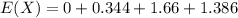
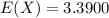
So
![V(X) = 3.3900 - [1.636]^2](https://img.qammunity.org/2021/formulas/mathematics/high-school/azzp5sqdv59ta3atg4qqjl2o4593vxik4d.png)
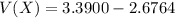
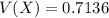
So