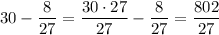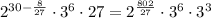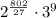Answer:

Explanation:
I will try to give as many details as possible.
First of all, I just would like to say:
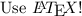
Texting in Latex is much more clear and depending on the question, just writing down without it may be confusing or ambiguous. Be together with Latex! (*^U^)人(≧V≦*)/
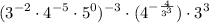
Note that
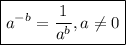
The denominator can't be 0 because it would be undefined.
So, we can solve the expression inside both parentheses.
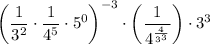
Also,
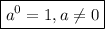
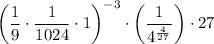
Note
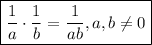
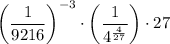
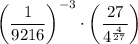
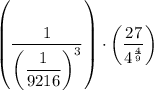
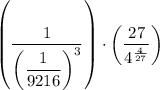
Note
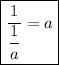
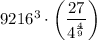
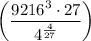
Once
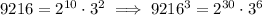
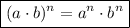
And
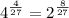
We have
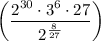
Also, once
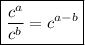
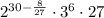
As