Question

A stone is catapulted at time t = 0, with an initial velocity of magnitude 21.1 m/s and at an angle of 39.9° above the horizontal. What are the magnitudes of the (a) horizontal and (b) vertical components of its displacement from the catapult site at t = 1.08 s? Repeat for the (c) horizontal and (d) vertical components at t = 1.75 s, and for the (e) horizontal and (f) vertical components at t = 5.09 s. Assume that the catapult is positioned on a plain horizontal ground.

Answer 1

(a) X = 17.48 m

(b) Y = 8.903 m

(c) X = 28.33 m

(d) Y = 8.68 m

(e) X = 44.68 m

(f) Y = 0 m

Step-by-step explanation:

Given;

magnitude of initial velocity, v = 21.1 m/s

angle of projection, θ = 39.9°

the horizontal component of the velocity,
`v_x = vcos \theta`

`v_x = 21.1(cos 39.9^0) = 16.187 \ m/s`

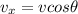
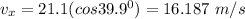
the vertical component of the velocity,
`v_y = vsin \theta`

`v_y = 21.1(sin 39.9^0) = 13.535 \ m/s`

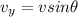
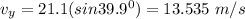
(a) the horizontal components of its displacement;

`X = v_xt + (1)/(2) gt^2`

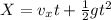
gravitational influence on horizontal direction is negligible, g = 0

`X = v_xt \\\\X = (16.187)(1.08)\\\\X = 17.48 \ m`

(b) the vertical components of its displacement;

`Y = v_yt + (1)/(2) gt^2\\\\Y = (13.535*1.08) + (1)/(2) (-9.8)(1.08)^2\\\\Y = 14.618 -5.715\\\\Y = 8.903 \ m\\`

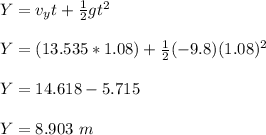
(c) the horizontal components of its displacement;

`X = v_xt\\\\ X = (16.187)(1.75)\\\\X = 28.33 \ m`

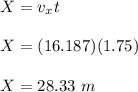
(d) the vertical components of its displacement;

`Y = v_yt + (1)/(2) gt^2\\\\Y = (13.535 *1.75) + (1)/(2) (-9.8)(1.75)^2\\\\Y = 8.68 \ m`

(e) the horizontal components of its displacement;

`X = v_xt \\\\X = (16.187*5.09)\\\\X = 82.39 \ m\\`

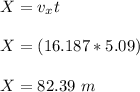
(f) the vertical components of its displacement;

`Y = v_yt + (1)/(2)gt^2\\\\ Y = (13.535*5.09)+ (1)/(2)(-9.8)(5.09)^2\\\\Y = -58.1 \ m`

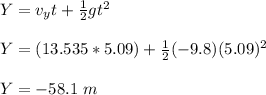
this displacement is not possible because it is beyond zero vertical level; it shows that the stone will hit the ground before 5.09 s.

When the stone hits the ground Y = 0 m

At zero vertical displacement (Y = 0 m), the time at that position will be calculated as;

`Y = v_yt+(1)/(2)gt^2\\\\0 = (13.535t) + (1)/(2)(-9.8)t^2\\\\0= 13.535t - 4.9t^2\\\\0 = t(13.535-4.9t)\\\\t = 0 \ \ or \\\\13.535-4.9t = 0\\\\4.9t = 13.535\\\\t = 2.76 \ s`

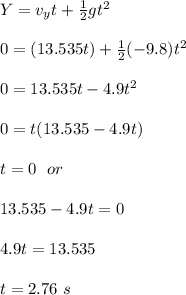
The horizontal displacement at this time is given by;

X = vₓt

X = (16.187 x 2.76)

X = 44.68 m