Question

Country Financial, a financial services company, uses surveys of adults age and older to determine if personal financial fitness is changing over time (USA Today, April 4, 2012). In February of 2012, a sample of adults showed indicating that their financial security was more than fair. In February of 2010, a sample of adults showed indicating that their financial security was more than fair. a. State the hypotheses that can be used to test for a significant difference between the population proportions for the two years.\

Answer 1

Complete Question

Country financials, a financial services company, uses surveys of adults age 18 and older to determine if personal financial fitness is changing over time. In February 2012, a sample of 1000 adults showed 410 indicating that their financial security was more that fair. In Feb 2010, a sample of 900 adults showed 315 indicating that their financial security was more than fair.

a

State the hypotheses that can be used to test for a significant difference between the population proportions for the two years.

b

What is the sample proportion indicating that their financial security was more that fair in 2012?In 2010?

c

Conduct the hypothesis test and compute the p-value.At a .05 level of significance what is your conclusion?

Answer:

a

The null hypothesis is
`H_o : p_1 = p_2`

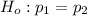
The alternative hypothesis is
`H_a : p_1 \\e p_2`

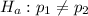
b

in 2012
`\r p_1 =0.41`

in 2010
`\r p_2 =0.35`

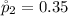
c

The p-value is
`p-value = 0.0072`

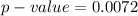
The conclusion is

There is sufficient evidence to conclude that the proportion of those indicating that financial security is more fair in Feb 2010 is different from the proportion of those indicating that financial security is more fair in Feb 2012.

Explanation:

From the question we are told that

The sample size in 2012 is
`n_1 = 1000`

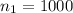
The number that indicated that their finance was more than fail is k = 410

The sample size in 2010 is
`n_2 = 900`

The number that indicated that their finance was more than fail is u = 315

The level of significance is
`\alpha  =  0.05[/ex]</p><p>The null hypothesis is  [tex]H_o : p_1 = p_2`

The alternative hypothesis is
`H_a : p_1 \\e p_2`

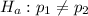
Generally the sample proportion for 2012 is mathematically represented as

`\r p_1 = (k)/(n_1)`

=>
`\r p_1 = (410)/(1000)`

=>
`\r p_1 =0.41`

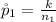
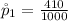
Generally the sample proportion for 2010 is mathematically represented as

`\r p_2 = (u)/(n_2)`

=>
`\r p_2 = (315)/(900)`

=>
`\r p_2 =0.35`

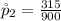
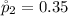
Generally the pooled sample proportion is mathematically represented as

`\r p = (k + u )/(n_1 + n_2)`

=>
`\r p =  (410 + 315 )/(1000+ 900)`

=>
`\r p = 0.3816`

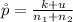
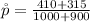
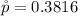
Generally the test statistics is mathematically represented as

`z = \frac{( \r p_1 - \r p_2 ) - 0}{\sqrt{\r p (1 - \r p ) ( (1)/(n_1) +(1)/(n_2) )} }`

`z = \frac{( 0.41 -0.35 ) - 0}{\sqrt{0.3816 (1 - 0.3816 ) ( (1)/(1000) +(1)/(900) )} }`

`z = \frac{( 0.41 -0.35 ) - 0}{\sqrt{0.3816 (1 - 0.3816 ) ( (1)/(1000) +(1)/(900) )} }`

`z  =  2.688`

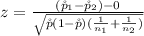
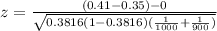
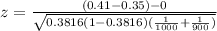
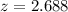
Generally the p- value is mathematically represented as

`p-value = 2 P(Z >2.688  )`

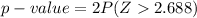
From the z -table

`P(Z > 2.688) = 0.0036`

So

`p-value = 2 *0.0036`

`p-value = 0.0072`

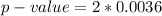
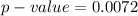
So from the p-value obtained we see that p-value <
`\alpha` so we reject the null hypothesis

Thus there is sufficient evidence to conclude that the proportion of financial security is more fair in Feb 2010 is different from the proportion of financial security is more fair in Feb 2012.