Question

Duke Energy reported that the cost of electricity for an efficient home in a particular neighborhood of Cincinnati, Ohio was $104 per month (Home Energy Report, Duke Energy, March, 2012). A researcher believes that the cost of electricity for a comparable neighborhood in Chicago, Illinois is higher. A sample of homes in this Chicago neighborhood will be taken and the sample mean monthly cost of electricity will be used to test the following null and alternative hypotheses.

Assume the sample data lead to rejection of the null hypothesis.
What would be your conclusion about the cost of electricity in the Chicago neighborhood?
The input in the box below will not be graded, but may be reviewed and considered by your instructor. What is the Type I error in this situation?
The Type 1 error in this situation What are the consequences of making this error?
The input in the box below will not be graded, but may be reviewed and considered by your instructor. What is the Type II error in this situation?

Answer 1

When the null hypothesis is rejected

The conclusion is that there is enough evidence to support the claim of the researcher

When a type I error occurs

The consequences is that the conclusion that there is enough evidence to support the claim of the researcher is actually incorrect

When a type II error occurs

The consequences is that the conclusion that there is enough evidence to support the claim of the researcher is actually correct

Explanation:

From the question we are told that

The cost of electricity per month is
`\mu = \$104`

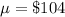
The null hypothesis is
`H_o : \mu = \$104`

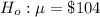
The alternative hypothesis is
`H_o :  \mu  >   \$104`

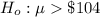
Generally if the null hypothesis is rejected then the conclusion would be that there is enough evidence to support the claim of the researcher

Generally a Type I error is a an error that occurs when the null hypothesis is incorrectly rejected

So in the case of this question the consequence of making this type of error is that the conclusion that there is enough evidence to support the claim of the researcher is actually incorrect

Generally a Type II error is an error that occurs when the null hypothesis is incorrectly not rejected

So in the case of this question the consequence of making this type of

error is that the conclusion that there is enough evidence to support the claim of the researcher is actually correct