Question

Twenty distinct cars park in the same parking lot every day. Ten of these cars are USmade while the other ten are foreign-made. The parking lot has exactly twenty spaces all in a row so the cars park side by side. However, the drivers have varying schedules so the position any car might take on a certain day is random. What is the probability that on a given day, the cars will park in such a way that they alternate (i.e., no two US-made cars are adjacent and no two foreign-made cars are adjacent)?

Answer 1

The probability that on a given day, the cars will park in such a way that they alternate is 1.0825 × 10⁻⁵.

Explanation:

It is provided that the cars will be parked in such a way that they will be alternating: US made, foreign made, US made, foreign made, etc.

First park all the US cars. This can be done in 10! ways, since the cars are distinct.

Now park the foreign cars between the US cars. This can also be done in 10! ways.

Since the sequence could begin either with a US car or with a foreign car, the possible number of ways to park alternating cars is

Favorable Outcomes = 2 × 10! × 10!

The total number of ways to park the 20 distinct cars is,

Total Outcomes = 20!

Compute the probability that on a given day, the cars will park in such a way that they alternate as follows:

`P(\text{Alternate Parking})=\frac{\text{Favorable Outcomes}}{\text{Total Outcomes}}`

`=(2* 10!* 10!)/(20!)\\\\=(2* 10!* 10!)/(20* 19* 18* ...10!)\\\\=(2* 10!)/(20* 19* 18* ...11)\\\\=1.0825* 10^(-5)`

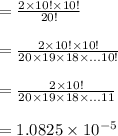
Thus, the probability that on a given day, the cars will park in such a way that they alternate is 1.0825 × 10⁻⁵.