Question

Suppose a university advertises that its average class size is 32 or less. A student organization is concerned that budget cuts have led to increased class sizes and would like to test this claim. A random sample of 40 classes was​ selected, and the average class size was found to be 34.8 students. Assume that the standard deviation for class size at the college is 99 students. Using α=0.10​, complete parts a and b below.a. Does the student organization have enough evidence to refute the​ college's claim?Determine the null and alternative hypotheses.Upper H 0H0​:μ▼Upper H 1H1​:μ▼

Answer 1

a

The student does have enough evidence to refute the college claim

b

The null hypothesis is
`H_o : \mu \le 32`

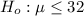
The alternative hypothesis is
`H_a : \mu > 32`

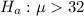
Explanation:

From the question we are told that

The average class size is
`\mu = 32`

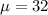
The sample size is
`n = 40`

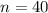
The sample mean is
`\= x = 34.8`

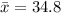
The standard deviation is
`\siigma = 99`

The significance level is
`\alpha = 0.10`

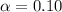
The null hypothesis is
`H_o : \mu \le 32`

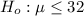
The alternative hypothesis is
`H_a : \mu > 32`

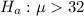
Generally the test statistics is mathematically represented as

`z =(\= x - \mu)/( (\sigma )/(√(n) ) )`

=>
`z = (34.8 - 32)/( (99 )/(√(99) ) )`

=>
`z = 0.1789`

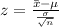
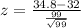
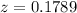
Generally the p-value is mathematically represented as

`p- value = P (Z > 0.1789)`

From the z- table

`P (Z > 0.1789) =0.42901`

So

`p- value = 0.42901`

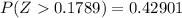
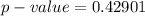
So from the calculation we can see that
`p- value > \alpha` so we fail to reject the null hypothesis

This means that the student does not have enough evidence to refute the college claim