Answer:
 and
and

Step-by-step explanation:
According to Coulomb's law, the magnitude of force between two point object having change
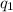 and
and
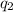 and by a dicstanced is
and by a dicstanced is
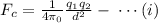
Where,
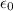 is the permitivity of free space and
is the permitivity of free space and
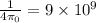 in SI unit.
in SI unit.
Before dcollision:
Charges on both the sphere are
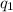 and
and
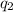 , d=20cm=0.2m, and
, d=20cm=0.2m, and
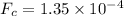 N
N
So, from equation (i)
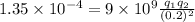
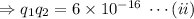
After dcollision: Each ephere have same charge, as at the time of collision there was contach and due to this charge get redistributed which made the charge density equal for both the sphere t. So, both have equal amount of charhe as both are identical.
Charges on both the sphere are mean of total charge, i.e
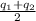
d=20cm=0.2m, and
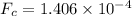 N
N
So, from equation (i)
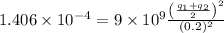
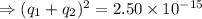

As given that the force is repulsive, so both the sphere have the same nature of charge, either positive or negative, so, here take the magnitude of the charge.
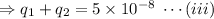
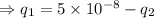
The equation (ii) become:
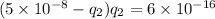

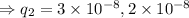
From equation (iii)
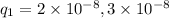
So, the magnitude of initial charges on both the sphere are
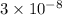 Coulombs
Coulombs
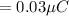 and
and
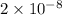 Colombs or
Colombs or
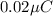 .
.
Considerion the nature of charges too,
 and
and
