Answer:
(1) The cost formula is: y = $19,050 + $12·x.
(2) The cost of moving materials if 340 moves are made is $23,130.
(3) 82.81% of the variability in moving cost is explained by the number of moves.
Explanation:
The computer output for the regression analysis of 80 data points is as follows:
Intercept: $19,050
Slope: 12
Coefficient of correlation: 0.91
Standard error: $220
(1)
The general formula of regression equation is:
y = a + b·x
Here,
a = intercept
b = slope
The cost formula is:
y = $19,050 + $12·x
(2)
Predict the cost of moving materials if 340 moves are made as follows:
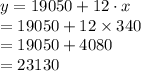
Thus, the cost of moving materials if 340 moves are made is $23,130.
(3)
The coefficient of determination R² specifies the percentage of the variance in the dependent variable (Y) that is forecasted or explained by linear regression and the forecaster variable (X, also recognized as the independent-variable).
The coefficient of determination R² can be computed by squaring the correlation coefficient value.
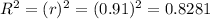
Thus, 82.81% of the variability in moving cost is explained by the number of moves.