Question

Recall from Intermediate Algebra that two non-vertical lines are perpendicular if and only if they have negative reciprocal slopes. That is to say, if one line has slopem1and the other has slopem2thenm1 · m2 = −1.Please note that a horizontal line is perpendicular to a vertical line and vice versa, so we assumem1 ≠ 0andm2 ≠ 0.Below, you are given a line and a point which is not on that line. Find the line perpendicular to the given line which passes through the given point.

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The line is
`y = -4 x`

Explanation:

From the question we are told that

The line is
`y = (1)/(4) x + 8`

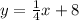
The point is P(0,0 )

Generally the equation for a line is
`yn = mx + c`

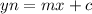
Now comparing this with the given equation we see that

`m =(1)/(4) = slope`

`C =8 = intercept`

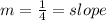
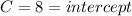
Generally the slope of the perpendicular to the given line is mathematically evaluated as

`m_1 = - (1)/(m)`

=>
`m_1 = - (1)/( (1)/(4))`

=>
`m_1 = -4`

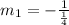
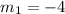
Generally from the univesal equation of a line and the given point we have that

y = mx + c at p(0,0) and
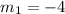`m_1 = -4` is

0 = -4 (0 ) + c

=> c = 0

Hence the equation perpendicular to the line given at the point given is

`y = -4 x`