Question

The rate at which heat enters an air conditioned building is often roughly proportional to the difference in temperature between inside and outside.

(a) Under this assumption, show that the cost of operating an air con- ditioner is proportional to the square of the temperature difference.
(b) Give a numerical example for a typical house and discuss implications for your electric bill.
(c) Suppose instead that heat enters the building at a rate proportional to the square-root of the temperature difference between inside and outside. How would the operating cost now depend on the temperature difference?

Answer 1

Considering first question

Generally the coefficient of performance of the air condition is mathematically represented as

`COP  =  (T_i)/(T_o - T_i)`

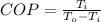
Here
`T_i` is the inside temperature

while
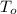`T_o` is the outside temperature

What this coefficient of performance represent is the amount of heat the air condition can remove with 1 unit of electricity

So it implies that the air condition removes
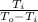`(T_i)/(T_o - T_i)` heat with 1 unit of electricity

Now from the question we are told that the rate at which heat enters an air conditioned building is often roughly proportional to the difference in temperature between inside and outside. This can be mathematically represented as

`Q \ \alpha \ (T_o - T_i)`

=>
`Q= k (T_o - T_i)`

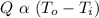
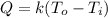
Here k is the constant of proportionality

So

since 1 unit of electricity removes
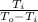`(T_i)/(T_o - T_i)` amount of heat

E unit of electricity will remove
`Q= k (T_o - T_i)`

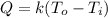
So

`E =  (k(T_o - T_i))/((T_i)/( T_h - T_i) )`

=>
`E = (k)/(T_i) (T_o - T_i)^2`

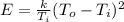
given that
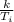`(k)/(T_i)` is constant

=>
`E \  \alpha  \  (T_o - T_i)^2`

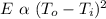
From this above equation we see that the electricity required(cost of powering and operating the air conditioner) is approximately proportional to the square of the temperature difference.

Considering the second question

Assuming that
`T_i   =  30 ^oC`

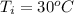
and
`T_o  =  40 ^oC`

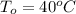
Hence

`E = K (T_o - T_i)^2`

Here K stand for a constant

So

`E = K (40 -  30)^2`

=>
`E = 100K`

Now if the
`T_i   =  20 ^oC`

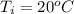
Then

`E = K (40 -  20)^2`

=>
`E = 400 \ K`

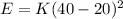
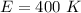
So from this see that the electricity require (cost of powering and operating the air conditioner)when the inside temperature is low is much higher than the electricity required when the inside temperature is higher

Considering the third question

Now in the case where the heat that enters the building is at a rate proportional to the square-root of the temperature difference between inside and outside

We have that

`Q = k (T_o - T_i )^{(1)/(2) }`

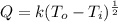
So

`E =  \frac{k (T_o - T_i )^{(1)/(2) }}{(T_i)/(T_o - T_i) }`

=>
`E =  (k)/(T_i) * (T_o - T_i) ^{(3)/(2) }`

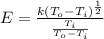
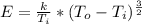
Assuming
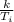`(k)/(T_i)` is a constant

Then

`E \ \alpha \ (T_o - T_i)^{(3)/(2) }`

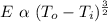
From this above equation we see that the electricity required(cost of powering and operating the air conditioner) is approximately proportional to the square root of the cube of the temperature difference.