Question

You are piloting a General Aviation aircraft (e.g. Cessna 172) over the Georgia Tech campus in level flight at 3000 ft altitude. Your airspeed indicator shows that the true airspeed is 100 knots. You have trimmed the aircraft to have no sideslip and pitch angle at a 3 degree angle of attack. Your magnetic compass (which is uncorrected for magnetic variation) indicates that you are flying in the direction of local magnetic East. A local weather forecast predicted the winds to be steady at 10 knots coming exactly from the northeast direction at the time you took off.

a. Using the information provided above and any additional information you may require (state what it is), determine your aircraft's north and east velocity components, Vn and ve, in knots. Starting from Tech Tower at t = 0, you continue in this direction and you are planning to fly directly over a local VOR beacon exactly 10 minutes later. However, you note that you don't pass directly over the beacon and after 10 minutes and 15 seconds have elapsed you are exactly 300 meters away from the VOR beacon in the Easterly direction.
b. Assuming the discrepancy is attributable only to wind speed, estimate the actual average wind speed components, Vwind-n and Vwind-e in knots. Use a flat Earth approximation.
c. Based on the instruments you are using, describe 3 common causes of measurement error that could affect the output of either sensor.

Answer 1

a) vₓ = 100 + 7.07 = 107.07 knot (East) , v_{y} = 7.07 knot (North)

b) v_wind_ North = 0 , v_wind_West = 61.12 knot (West)

Step-by-step explanation:

a) This is a vector velocity addition problem, they tell us that the plane goes East at 100 Knots and the wind goes North East at 10 Knots

the components ask the total speed of the plane.

For this we decompose the wind speed

cos 45 = v₂ₓ / V₂

sin 45 =
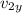`v_(2y)` / v₂

v₂ₓ = v₂ cos 45

v_{2y} = v₂ sin 45

v₂ₓ = 10 cos 45 = 7.07 m / s

v_{2y} = 10 sin45 = 7.07 m / s

the speed of the plane is

vₓ = v_plane + v₂ₓ

v_{y} = v_{2y}

vₓ = 100 + 7.07 = 107.07 knot (East)

v_{y} = 7.07 knot (North)

speed is

v = (107.07 i ^ + 7.07 j ^) knot

b) Estimated time for Target VOR t = 10 min

for a time of t = 10 min and 15 s, it is at a distance of d = 300 m from the VOR in an easterly direction

find the average speed of time on the ride

in the North direction there is no deviation so the average wind speed is zero

v_wind_ North = 0

In the east direction

as the estimated time was 10 min and the real time for the distance is 10 min 15 s

the time difference is t = 15 s to travel d = 300 m

with these data we can calculate the speed of the plane

v = x / t

v = 300/15

v = 20 m / s

let's reduce this speed to knot

v_real = 20 m / s (1knot / 0.5144 m / s) = 38.88 knots

therefore the wind speed is

v_tral = v_plane + v_wind_Este

v_wind_Este = v_real - v_avión

v_wind_Este = 38.88 - 100

v_wind_Este = -61.12 knot

the negative sign indicates that the wind is going west

v_wind_West = 61.12 knot (West)

3)

* The compass is not calibrated, to correct the magnetic deviation, therefore it gives an appreciable error in the direction

* The wind speed is taken when leaving, but there is no constant monitoring, so a change in direction or wind speed in the trajectory can significantly affect the results.

* The aircraft may noir throughout the trajectory at level, due to pitch errors