Question

A bacteria population increases exponentially at a rate of r% each day. After

32 days, the population has increased by 309%. Find the value of r.

Answer 1

r=4.5% daily

Explanation:

Exponential Growth

The natural growth of some magnitudes can be modeled by the equation:

`P=P_o(1+r)^t`

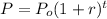
Where P is the actual amount of the magnitude, Po is its initial amount, r is the growth rate and t is the time.

We know after t=32 days, the population has increased by 309%. Being the original population P the 100%, then the population reached 309+100= 409%.

Substitute the given values into the model function:

`409\%P_o=100\%P_o(1+r)^(32)`

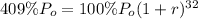
Simplifying:

`4.09=(1+r)^(32)`

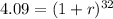
We need to solve for r. Taking the 32nd root:

`\sqrt[32]{4.09}=\sqrt[32]{(1+r)^(32)}`

Simplifying:

`1+r=\sqrt[32]{4.09}=1.045`

Solving:

`r=1.045-1\Rightarrow r=0.045`

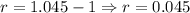
r=4.5% daily