Question

A hockey player whacks a 162-g puck with her stick, applying a 171-N force that accelerates it to 42.3 m/s. A. If the puck was initially at rest, for how much time did the acceleration last? B. The puck then hits the curved corner boards, which exert a 151-N force on the puck to keep it in its circular path. What’s the radius of the curve?

Answer 1

Given parameters:

Mass of puck = 162g = 0.162kg (1000g = 1kg)

Force exerted on puck = 171N

Final velocity = 42.3m/s

Unknown

A. time of the acceleration

B. radius of the curve?

Solution:

A. time of the acceleration

the initial velocity of the puck = 0m/s

We know that;

Force = mass x acceleration

Acceleration =
`(Final velocity - Initial velocity)/(time taken)`

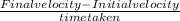
Acceleration =
`(42.3 - 0)/(t)`

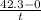
So force = mass x
`(42.3 )/(t)`

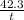
Input the parameters and solve for time;

171 = 0.162 x
`(42.3 )/(t)`

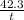
171 =
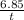
`(6.85)/(t)`

t =
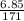`(6.85)/(171)` = 0.04s

The time of acceleration is 0.04s

B. radius of the curve;

to solve this, we apply the centripetal force formula;

F =
`(mv^(2) )/(r)`

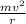
where;

F is the centripetal force

m is the mass

v is the velocity

r is the radius

Since the force exerted on the puck is 151;

input the parameters and solve for r²;

151 =
`(0.162 x 42.3^(2) )/(r)`

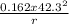
151r = 0.162 x 42.3²

r = 1.92m

The radius of the circular curve is 1.92m