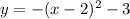Question

What is the equation of the following graph

Answer 1

`y=-(x-2)^2-3`

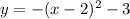
Explanation:

Equation of the Quadratic Function

The vertex form of the quadratic function has the following equation:

`y=a(x-h)^2+k`

Where (h, k) is the vertex of the parabola that results when plotting the function, and a is a coefficient different from zero.

The graph provided in the question has two clear points:

The vertex, located at (2,-3)

The y-intercept, located at (0,-7)

Substituting the coordinates of the vertex, the equation of the function is:

`y=a(x-2)^2-3`

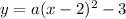
The value of a will be determined by using the other point:

`-7=a(0-2)^2-3`

Operating:

`-7=a(4)-3`

`4a=-4\Rightarrow a=-4/4`

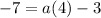
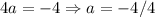
Solving:

a=-1

The equation of the graph is:

`y=-(x-2)^2-3`