Answer:
a) y = 16.51 [m]
b) t = 1.83 [s]
Step-by-step explanation:
To solve this problem we must use two kinematics equations, the first to determine the height to which the ball reaches, and the second equation to determine how long it lasts in the air.
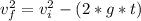
where:
Vf = final velocity = 0
Vi = initial velocity = 18 [m/s]
g = gravity acceleration = 9.81[m/s^2]
t = time [s]
Note: the negative sign of the Equation indicates that the acceleration of gravity acts in the opposite direction to the movement of the ball. The final velocity is zero, since the ball reaches its maximum altitude when the velocity is zero.
Now replacing:
0 = (18)^2 - (2*9.81*y)
y = 16.51 [m]
b)
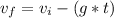
0 = 18 - (9.81*t)
t = 1.83 [s]