Question

Pls help ...................

Answer 1

Answer: Choice D

=======================================================

Step-by-step explanation:

Start by graphing the system of equations

`\begin{cases}x-y = 6\\2x+5y = -4\\ x = -1\end{cases}`

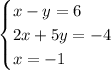
This is represented as the boundary lines. The first two equations produce solid boundary lines. The last equation makes a dashed boundary line. We use solid boundary lines whenever "or equal to" is involved with the inequality sign.

Note how 7 separate regions result from the intersecting lines. Check out the diagram below to see the different regions.

--------------------------

To graph
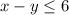`x-y \le 6` which is the same as
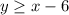`y \ge x-6`, we will shade in regions 1, 2, 4 and 5. All of these regions are above the boundary line y = x-6

Ignore any other region (3,6, and 7) since they don't make the first inequality true.

Of regions 1, 4, 5 and 6, only regions 4 and 5 are below the boundary line 2x+5y = -4. So we cross off regions 1 and 6.

We're now down to just two regions: 4 and 5

We cross off region 5 because it is not to the right of the vertical line x = -1

All that's left is region 4. Any point in region 4 makes all of the three original inequalities true.

So the solution will only have region 4 shaded like choice D shows.