Question

Again help, i don’t understand this at all

Answer 1

The difference quotient of f is 8. Option C

Step-by-step explanation:

Difference Quotient

Given a function f(x), the difference quotient is defined as

`\displaystyle d=(f(h+h)-f(x))/(h),\ h\\eq 0`

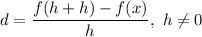
The function provided in the question is

`f(x)=8x+1`

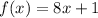
Find f(x+h) by substituting x by x+h:

`f(x+h)=8(x+h)+1`

`f(x+h)=8x+8h+1`

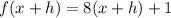
Now compute:

`\displaystyle d=(8x+8h+1-(8x+1))/(h)`

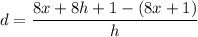
Operating:

`\displaystyle d=(8x+8h+1-8x-1)/(h)`

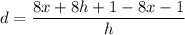
Simplifying:

`\displaystyle d=(8h)/(h)`

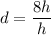
d=8

A. Incorrect.

This choice is different from the answer.

B. Incorrect.

This choice is different from the answer.

C. Is correct

The difference quotient is 8 as explained above.

D. Incorrect.

This choice is different from the answer.