Answer:
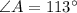
Explanation:
We know that ∠A and ∠B are vertical angles.
Remember that vertical angles have the same measure. So:
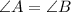
Substitute them for their equations:
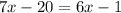
Solve for x. Add 20 to both sides:
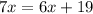
Subtract 6x from both sides. So, the value of x is:
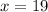
To find ∠A, we can use its equation again:
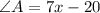
Substitute 19 for 7:
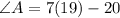
Multiply and subtract:

So, the value of ∠A is 113°.
And we're done!