Given:
The growth of a sample of bacteria can be modeled by the function
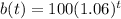
where, b is the number of bacteria and t is time in hours.
To find:
The number of total bacteria after 3 hours.
Solution:
We have,
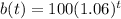
Here, b(t) number of total bacteria after t hours.
Substitute t=3 in the given function, to find the number of total bacteria after 3 hours.

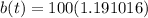
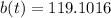
Therefore, the number of total bacteria after 3 hours is 119.1016.