Question

AP CAL AB!!!! HELP. A ladder 10 feet long rests against a vertical wall. Let θ be the angle between the top of the ladder and the wall, and let x be the distance from the bottom of the ladder to the wall. If the bottom of the ladder slides away from the wall, how fast does x change with respect to θ when θ=π/3 ?

Answer 1

`\displaystyle (dx)/(d\theta)=5\text{ ft/rad}`

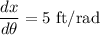
Explanation:

Please refer to the diagram below.

We can use the sine function. Recall that the sine function is the ratio between the opposite side and the hypotenuse. Hence:

`\displaystyle \sin(\theta)=(x)/(10)`

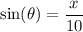
We want to find how fast x changes with respect to θ. So, we want to find dx/dθ. Therefore, let's take the derivative of both sides with respect to θ:

`\displaystyle (d)/(d\theta)[\sin(\theta)]=(d)/(d\theta)\left[(1)/(10)x\right]`

Differentiate. Since it's with respect to θ, we can differentiate the left-hand side like normal. On the right, we will implicitly differentiate. This yields:

`\displaystyle \cos(\theta)=(1)/(10)(dx)/(d\theta)`

Multiply both sides by 10. So, dx/dθ is:

`\displaystyle (dx)/(d\theta)=10\cos(\theta)`

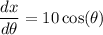
We want to find dx/dθ when θ is π/3. Thus, substitute π/3 for θ:

`\displaystyle (dx)/(d\theta)=10\cos\left((\pi)/(3)\right)`

Evaluate:

`\displaystyle (dx)/(d\theta)=10\left((1)/(2)\right)=5\text{ ft/rad}`

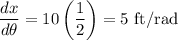
So, x is changing with respect to θ at a rate of 5 feet per radian.