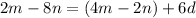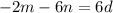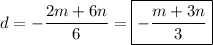Question

The third term of an A.P is 4m - 2n. If the ninth term of the progression is 2m - 8n. Find the common difference in terms of m and n​

Answer 1

Let
`a_n` denote the n-th term in the progression. So

`a_n=a_(n-1)+d`

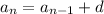
for some constant difference between terms d.

Solve for
`a_n` explicitly:

`a_4=a_3+d`

`a_5=a_4+d=a_3+2d`

`a_6=a_5+d=a_3+3d`

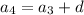
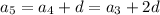
and so on, up to

`a_n=a_3+(n-3)d`

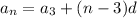
We're told that the third term is
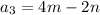`a_3=4m-2n`, and the ninth term is
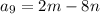`a_9=2m-8n`, and according to the recursive rule above, we have

`a_9=a_3+6d`

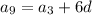
Solve for d :

`2m-8n=(4m-2n)+6d`

`-2m-6n=6d`

`d=-\frac{2m+6n}6=\boxed{-\frac{m+3n}3}`