Question

`\overline{AB}` and
`\overline{ED}` are parallel. What is the measure of
`\angle ABC`

A)
`45^\circ`
B)
`65^\circ`
C)
`55^\circ`
D)
`50^\circ`

Answer 1

`\tt Step-by-step~explanation:`

To find the measure of ∠ABC, we need to know that the sum of the interior angles of a triangle is 180º.

`\tt Step~1:`

Triangle CED has two given angles: 65º and 50º. We can add them together and subtract that from 180 to get the third measure.

`\tt 65+50=115\\180-115=65`

`\tt Step~2:`

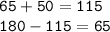
Since lines AB and ED are parallel, that means m∠ACB is also 65º since the vertical angle is also 65º. Then, we can add 65 and 50 together and subtract that from 180 to get our answer.

`\tt 65+50=115\\180-115=65`

`\large\boxed{\tt Our~final~answer:~m\angle ABC=65~degrees }`

Answer 2

B: 65°

Explanation:

Step 1:

AB ║ ED Given

Step 2:

∠E = 65° Given

Step 3:

∠ABC = 65° Alt. Int. ∠'s ( Alternate Interior ∠'s)

Answer:

B: 65°

Hope This Helps :)